LOS DIVISORES Y SU CRITERIO DE DIVISIBILIDAD

Youtube: https://www.youtube.com/watch?v=8-TOxS-8ZnQ&feature=emb_title
Para definir qué son los divisores de un número se tomará el siguiente ejemplo: la división . El resultado es y sobra . Cuando un número que divide a otro produce un residuo de cero unidades, se dice que es divisor del número dividido. En este caso se puede decir que cuatro es divisor de doce, ya que el residuo de la operación , es igual a .

Como te puedes dar cuenta, se puede decir que un número es divisor de otro si está contenido una cantidad entera de veces. En el ejemplo anterior cuatro es divisor de doce porque está exactamente tres veces en él. Fíjate que las expresiones y están estrechamente relacionadas.
Recuerda que el símbolo se puede interpretar como “veces”. Así, la expresión se lee “ veces es igual a ”, y significa que está contenido veces en . De la expresión se puede decir que está veces en
Un número puede tener varios divisores, usaremos el símbolo para representar el conjunto de los divisores del numero Por ejemplo, en el caso del doce se tiene:
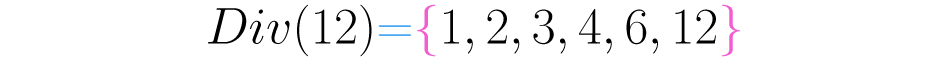
Observa que los números y producen un residuo de cero cuando se divide en cada uno de ellos.
Para representar la divisibilidad entre dos números se usa el símbolo así: se escribe para decir “seis divide a doce” o “seis es divisor de doce”. En general, la expresión significa “ divide a ” o “ es divisor de ”.
CRITERIOS DE DIVISIBILIDAD
Los criterios de divisibilidad son reglas que sirven para saber si un número es divisible por otro sin necesidad de realizar la división.
Aunque pueden buscarse criterios para todos los números, sólo expondremos los más comunes:Criterio de divisibilidad por 2
Un número es divisible por 2 si acaba en 0 o cifra par.
Ejemplos:
Números divisibles por 2: 36,94,521342,40,...
Criterio de divisibilidad por 3
Un número es divisible por 3 si la suma de sus cifras es múltiplo de 3.
Ejemplos:
Números divisibles por 3: 36,2142,42,...
Criterio de divisibilidad por 5
Un número es divisible por 5 si la última de sus cifras es 5 o es 0.
Ejemplos:
Números divisibles por 5: 35,2145,40,...
Criterio de divisibilidad por 9
Un número es divisible por 9 si la suma de sus cifras es múltiplo de 9.
Ejemplos:
Números divisibles por 9: 495,945,53640,...
Criterio de divisibilidad por 11
Debemos hacer lo siguiente:
Sumamos las cifras que ocupan lugares pares, sumamos las cifras que ocupan lugares impares. A la suma mayor le restamos la suma menor, si la diferencia es 0 o múltiplo de 11, entonces el número es múltiplo de 11.
Ejemplos:
Múltiplos de 11: 2343649,9889,18161902,...
Fuente : https://thales.cica.es/rd/Recursos/rd98/Matematicas/07/criterios.html
DIVISIÓN POR UNA CIFRA
Youtube: https://www.youtube.com/watch?v=PCRCrdJbaCM

Cómo se llama cada parte de la división
- Dividendo es el número que se va a dividir.
- Divisor es el número por el que se divide el dividendo.
- Cociente es el resultado de la división.
- Resto es la cantidad que sobra.

Vamos a entenderlo mejor con un caso práctico.
Imagina que quieres repartir 243 caramelos entre 5 amigos:
- El dividendo será 243 porque es la cantidad que queremos dividir.
- El divisor es 5 porque es el número por el que queremos dividir (repartir) los 243 caramelos.
- El cociente será el número de caramelos que recibe cada niño.
- El resto son los caramelos que sobran.
Pasos para calcular el cociente y el resto de una división
1. Cogemos la primera cifra del dividendo. Si esta cifra es más pequeña que el divisor, entonces tendremos que coger otra cifra más del dividendo.
En nuestro ejemplo la primera cifra del dividendo es 2, pero como es más pequeña que el divisor, que es 5, tenemos que coger otra cifra más: 24
2. Buscamos un número que al multiplicarlo por el divisor nos dé como resultado el dividendo. Si no lo hay, buscamos el resultado menor más próximo. El resultado de la multiplicación se resta al dividendo.
Nosotros tenemos que dividir 24 entre 5. Buscamos un número que multiplicado por 5 me dé 24. Como no es exacto buscamos el menor más próximo: 4 x 5 = 20. En este caso, 20 es el número más cercano a 24 siendo menor. Por lo tanto escribimos el 4 en el cociente y el 20 se lo restamos a 24, y 20 – 24 = 4
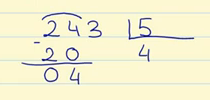
3. Bajamos la siguiente cifra del dividendo y realizamos de nuevo el paso 2.
Bajamos la siguiente cifra que es el 3. Con el 4 que ya teníamos y con el 3 que acabamos de bajar obtenemos el 43.
Ahora dividimos 43 entre 5. Buscamos un número que multiplicado por 5 nos dé 43. Como no es exacto buscamos un número que no dé el número menor más próximo. En este caso 5 x 8 = 40. Escribimos el 8 en el cociente y el 40 lo escribimos debajo del 43 para restarlo: 43 – 40 = 3.
Como no hay más cifras en el dividendo, hemos terminado la división.
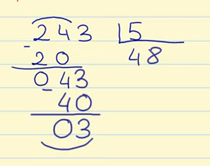
Por lo tanto, cada niño recibe 48 caramelos y sobran 3 caramelos sin repartir.
Si quieres ver una explicación más detallada de cómo dividir por una cifra y con más ejemplos visita nuestro tutorial de dividir por una cifra.
DIVISIÓN POR DOS CIFRAS
Video youtube: https://www.youtube.com/watch?v=6C-REXedOkY
1. Toma las primeras cifras del dividendo, el mismo número de cifras que tenga el divisor. Si el número que has tomado del dividendo es más pequeño que el divisor tienes que tomar la siguiente cifra del dividendo.
2. Divide el primer número del dividendo (o los dos primeros números si en el paso anterior has tenido que tomar otra cifra más) entre la primera cifra del divisor. Escribe el resultado de esa división en la parte del cociente.
3. Multiplica la cifra del cociente por el divisor, el resultado escríbelo debajo del dividendo y réstalo. Si no se puede porque el dividendo es más pequeño tendrás que escoger un número más pequeño en el cociente hasta que se pueda restar.
4. Una vez hecha la resta baja la cifra siguiente del dividendo y vuelve a repetir los pasos desde el punto 2, hasta que no queden más números en el dividendo.
Esta es la teoría, pero vamos a entenderlo mejor con un ejemplo:
Vamos a hacer la siguiente división de 2 cifras:

1. Toma las dos primeras cifras del dividendo: en este caso 57. Pero como 57 es más pequeño que 73 tienes que tomar otra cifra más: 573
2. Para dividir 573 entre 73 tomamos las dos primeras cifras del dividendo: 57 y lo dividimos entre la primera cifra del divisor:
57 : 7 = 8
3. Escribe el 8 en el cociente y multiplícalo por el divisor:
8 x 73 = 584
Pero 584 es mayor que 573, por lo tanto 8 «no cabe». Tienes que escoger el número anterior y volver a multiplicar:
7 x 73 = 511
511 es más pequeño que el dividendo, por lo tanto 7 «sí cabe». Escribimos 511 debajo de las cifras del dividendo y restamos:
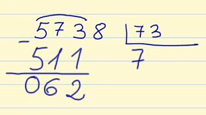
4. Baja la siguiente cifra del dividendo, que es el 8. Ahora tienes que dividir 628 entre 73. Hay que repetir los pasos anteriores:
Divide las dos primeras cifras del dividendo entre la primera cifra del divisor y escríbela en el cociente:
62 : 7 = 8
Multiplica esa cifra por el divisor:
8 x 73 = 584
584 es menor que 628, por lo tanto podemos hacer la resta:
628 – 584 = 44

El resultado de esta división es 78 y resto 44.
Dividir por 3
Paso 1. Ver el número de cifras que tiene el divisor.
Nuestro ejemplo tiene 3 cifras.
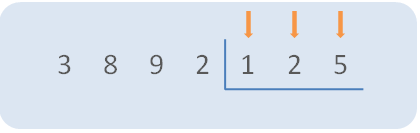
Paso 2. Tomar el mismo número de cifras que tiene el divisor en el dividendo.
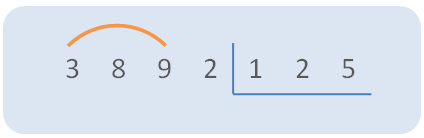
Paso 3. Comparar las 3 cifras del dividendo con las 3 cifras del divisor.
- Si el número de 3 cifras del dividendo es mayor, podemos empezar a dividir. En nuestro ejemplo, como 389 es mayor que 125, ¡empecemos a dividir!
- Si el número de 3 cifras del dividendo es menor que el número del divisor, tenemos que tomar una cifra más del dividendo. Más adelante veremos un ejemplo de este tipo.
Paso 4. Dividir las cifras del dividendo entre las cifras del divisor.
Dividir el primer número del dividendo (en nuestro ejemplo es el 3) entre el primer número del divisor (en nuestro ejemplo es el 1). 3 entre 1 es igual a 3. Multiplicamos nuestro divisor (125) por el 3 y vemos si cabe dentro de las 3 cifras del dividendo (389). 125 por 3 es igual a 375 y sí que cabe en (es menor que) las 3 cifras del dividendo. Colocamos el resultado debajo de las 3 cifras del dividendo y realizamos la resta.
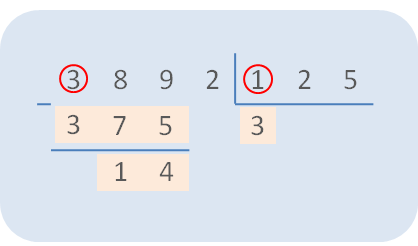
Paso 5. Bajar la cifra siguiente del dividendo y dividir como en el paso anterior hasta que no queden más cifras para bajar.
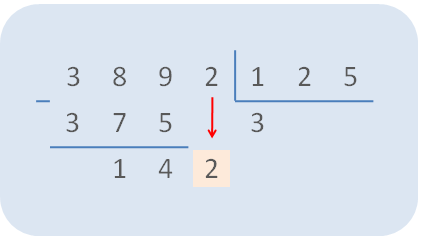
Habiendo bajado el 2, ahora dividimos 142 entre 125. Como la primera cifra de cada número es 1, probamos con el 1 y escribimos el 1 en el cociente. Multiplicamos 125 x 1 que nos da 125 y como 125 cabe dentro de 142 hacemos la resta.
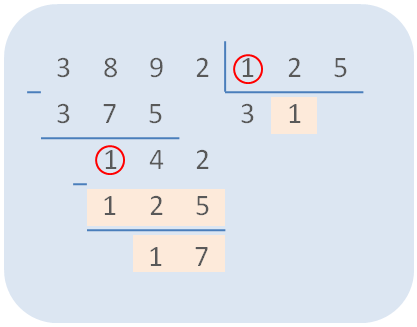
Nos hemos quedado sin más números para bajar en el dividendo. Ya hemos terminado de dividir 3892 entre 125.
El resultado es 31, que es el cociente, y nos queda un resto de 17.
Vamos a realizar rápidamente la comprobación para ver si no nos hemos equivocado por el camino. ¿Conoces la prueba para comprobar si una división hecha bien hecha?
Dividendo = divisor x cociente + resto
Vamos a usarla. ¿Cuánto nos da 125 x 31 + 17? Nos da 3892. Efectivamente nos da el mismo valor que el dividendo.
¡Comprobación realizada con éxito
PROPIEDAD DE LOS DIVISORES
Conocer las propiedades de los divisores te ayudará a familiarizarte con los mismos y a realizar las operaciones con más facilidad.
Todo número distinto de cero es divisor del mismo
Siempre que calcules los divisores de un número natural dado, encontrarás que el número en cuestión está en la lista de los divisores. Por ejemplo, los divisores de son: . Fíjate que el mismo hace parte de la lista de los divisores de , esto sucede con todos los números.
La razón por la que esto ocurre es la siguiente: dado un número , se tiene que . Es decir, que está una vez en , o que el residuo de la división es cero. Recuerda que precisamente esas son las condiciones que definen el ser divisor.
Esta propiedad se puede representar de varias formas:
- Para todo número distinto de cero, divide a .
- Para todo número distinto de cero .
Uno es divisor de todo número
¿Has notado que cuando se calculan los divisores de un número, siempre aparece el uno? Esto tiene una explicación: basta observar que para todo número se cumple . Por ejemplo, o . Es decir, uno está veces en . Por lo tanto .
Si un número es divisor de otros dos también lo es de su suma y de su diferencia
Tomemos como ejemplo los números , y . es divisor de y de , según esta propiedad también debe ser divisor de su suma: y de su resta: .
Como puedes ver en la siguiente imagen, hace parte del conjunto de divisores de y de .
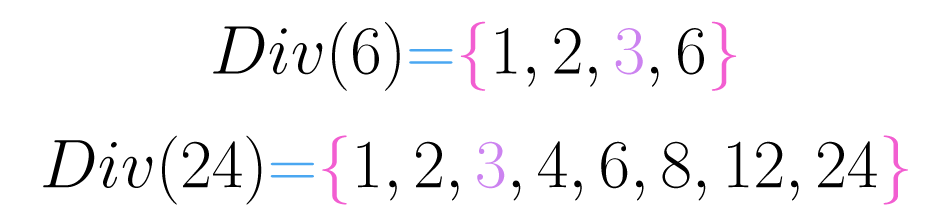
Podemos generalizar esta propiedad así: dados tres números cualesquiera , y si y , entonces y también .
Propiedad transitiva
Se puede enunciar esta propiedad así: si un número es divisor de otro y este lo es de un tercero, el primero es divisor del tercero.
Por ejemplo, es divisor de y a su vez es divisor de , la transitividad quiere decir que debe ser divisor de .
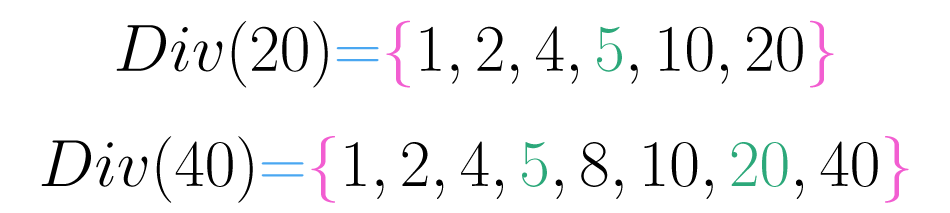
Nota que cada divisor de también es divisor de . Esta propiedad se generaliza así: dados tres números cualesquiera , y si y entonces .
ACTIVIDADES


muchas gracias profe 6-6
ResponderBorrar