NÚMEROS PRIMOS Y COMPUESTOS

¿Qué son los números primos?
Los números primos son aquellos que solo son divisibles entre ellos mismos y el 1.
¿Qué son los números compuestos?
Son aquellos números que además de ser divisibles por ellos mismos y la unidad, también son divisibles por otros números.
Vamos a ver un ejemplo de número primo y compuesto:
El 11 se puede escribir como la multiplicación de 1 x 11, pero no se puede escribir como ninguna otra multiplicación de números naturales. Solo tiene como divisores el 1 y el 11, por lo tanto es un número primo.
El 12 se puede escribir como la multiplicación de 1 x 12, y también se puede escribir como la multiplicación de 3 x 4, y de 2 x 6. Como 12 es divisible por más números de 1 y el mismo, 12 es un número compuesto.
Tabla de números primos
Vamos a construir la tabla de números primos hasta el 100.
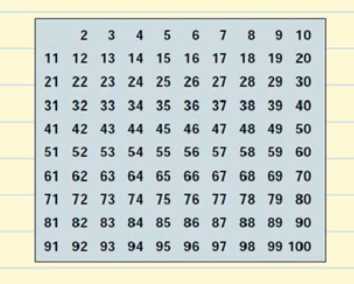
Vamos a empezar con el 2. El 2 es un número primo pero todos lo múltiplos de 2 serán números compuestos, ya que serán divisibles entre 2. Tachamos de nuestra tabla todos los múltiplos de 2.
El siguiente número primo es el 3, por lo tanto podemos tachar todos los múltiplos de 3, ya que serán números compuestos.
El siguiente número primo es el 5, por lo que tachamos todos los múltiplos de 5.
El siguiente número primo es el 7, así que tachamos todos los múltiplos de 7.
El siguiente número primo es el 11, por lo que tachamos todos los múltiplos de 11, que son el 22, 33, 44, 55, 66, 77, 88, y el 99. Todos estos ya habían sido tachados con anterioridad, por lo que ya hemos terminado de tachar todos los números compuestos de nuestra tabla.

Esta es nuestra lista de números primos del 1 al 100. No es necesario que te los aprendas de memoria, pero si que te acuerdes de los más pequeños, como el 2, 3, 5, 7, 11, 13.
Divisores de un número
El divisor de un número es el valor que divide al número en partes exactas, es decir, que el resto sea 0. Por ejemplo, vamos a calcular los divisores de 24.
Empezamos dividiendo entre los números:
24 / 1 = 24. Tanto 1 como 24 son sus divisores.
24 / 2 = 12. 2 y 12 son sus divisores.
24 / 3 = 8. 3 y 8 son sus divisores.
24 / 4 = 6. 4 y 6 son sus divisores.
24 / 5 = 4. No es una división exacta ya que el resto es 4, por lo tanto 5 no es un divisor.
El siguiente número es el 6, pero como ya tenemos el 6 como divisor de 24, ya hemos terminado de calcular los divisores de 24.
A continuación os proponemos una serie de ejercicios para practicar lo que hemos aprendido en este post sobre los número primos y compuestos.
Números compuestos

Ejemplos:
12 = 2 · 2 · 3
72 = 2 · 4 · 9
144 = 2 · 6 · 12
Los números compuestos se pueden expresar como productos de potencias de números primos. A dicha expresión se le llama descomposición de un número en factores primos.
Ejemplos:
12 = 2² · 3
72 = 2³ · 3²
144 = 24 · 3²
Factorizar un número
Para factorizar un número o descomponerlo en factores efectuamos sucesivas divisiones entre sus divisores primos hasta obtener un 1 como cociente.
Para factorizar utilizaremos una barra vertical, a la derecha escribimos los divisores primos y a la izquierda las sucesivas divisiones.
Ejemplo:
1Factorizar 2520
Como el número termina en cifra par es divisible por 2, colocamos el 2 a la derecha de la raya
Dividimos 2520 por 2 y lo colocamos a la izquierda
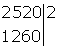
1260 termina en 0, por tanto también es divisible por 2, colocamos el 2 a la derecha de la raya
Dividimos 1260 por 2 y lo colocamos a la izquierda
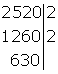
630 termina en 0, por tanto también es divisible por 2, colocamos el 2 a la derecha de la raya
Dividimos 630 por 2 y lo colocamos a la izquierda
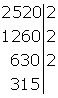
Como no to termina en cifra par ni en 0 no es divisible por 2, entonces probamos por 3. La suma de las cifras de 315 es igual a 9 que divisible por 3. Colocamos el 3 a la derecha de la raya
Dividimos 315 por 3 y lo colocamos a la izquierda
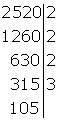
Volvemos a probar por 3. La suma de las cifras de 105 es igual a 6 que divisible por 3. Colocamos el 3 a la derecha de la raya
Dividimos 105 por 3 y lo colocamos a la izquierda
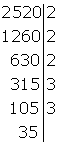
Volvemos a probar por 3. La suma de las cifras de 35 es igual a 7 que no es divisible por 3, por tanto tenemos que probar por el siguiente número primo que es 5, como 35 termina en 5 es divisible entre 5. Colocamos el 5 a la derecha de la raya
Dividimos 35 por 5 y lo colocamos a la izquierda
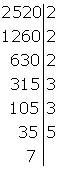
7 es un número primo, por tanto es divisible por sí mismo. Colocamos el 7 a la derecha de la raya
Dividimos 7 por 7 y lo colocamos a la izquierda
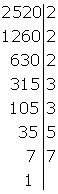
Una vez que llegamos a 1 termina la factorización
Como a la derecha tenemos el 2 repetido tres veces, el 3 repetido dos veces, el 5 y el 7; la factorización será:
Solución: 2 520 = 2³ · 3² · 5 · 7
2Factorizar 432
Ejemplo:

.gif)

Solución: 432 = 24 · 3³
ACTIVIDAD
.gif)
Comentarios
Publicar un comentario